阅读以下说明和C函数，将应填入(n)处的字句写在对应栏内。【说明】已知某二叉树的非叶子结点都有两个孩子结点，现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下：define MAXLEAFNUM 30struct node{char ch; /*当前结点表示的字符，对于非叶子结点，此域不用*/char *pstr; /*当前结点的编码指针，非叶子结点不用*/int parent; /*当前结点的父结点，为0时表示无父结点*/int lchild,rchild;/*当前结点的左、右孩子结点，为0时表示无对应的孩子结点*/};struct node Ht[2*MAXLEAFNUM]; /*数组元素Ht[0]不用*/该二叉树的n个叶子结点存储在下标为1～n的Ht数组元素中。例如，某二叉树如果其存储结构如下图所示，其中，与叶子结点a对应的数组元素下标为1，a的父结点存储在Ht[5]，表示为Ht[1].parent=5。Ht[7].parent=0表示7号结点是树根，Ht[7].child=3、Ht[7].rchild=6分别表示7号结点的左孩子是3号结点、右孩子是6号结点。如果用0或1分别标识二叉树的左分支和右分支(如上图所示)，从根结点开始到叶子结点为止，按所经过分支的次序将相应标识依次排列，可得到一个0、1序列，称之为对应叶子结点的编码。例如，上图中a，b，c，d的编码分别是100，101，0，11。函数LeafCode(Ht[],n)的功能是：求解存储在Ht中的二叉树中所有叶子结点(n个)的编码，叶子结点存储在Ht[1]～Ht[n]中，求出的编码存储区由对应的数组元素pstr域指示。函数LeafCode从叶子到根逆向求叶子结点的编码。例如，对上图中叶子结点a求编码的过程如下图所示。typedef enum Status {ERROR,OK} Status;【C函数】Status LeafCode(struct node Ht[], int n){int pc, pf; /*pc用于指出树中的结点，pf则指出pc所对应结点的父结点*/int i,start;char tstr[31] = {'\0'}; /*临时存储给定叶子结点的编码，从高下标开始存入*/for(i = 1;(1); i++){ /*对所有叶子结点求编码，i表示叶结点在HT数组中的下标*/start = 29;pc = i; pf = Ht[i].parent;while (pf !=(2)) { /*没有到达树根时，继续求编码*/if ((3).lchild == pc ) /*pc所表示的结点是其父结点的左孩子*/tstr[--start] = '0';elsetstr[--start] = '1';pc =(4); pf = Ht[pf].parent; /*pc和pf分别向根方向回退一层*/}/* end of while */Ht[i].pstr = (char *) malloc(31-start);if (!Ht[i].pstr) return ERROR;strcpy(Ht[i].pstr,(5));}/* end of for */return OK;}/* and of LeafCode */
阅读以下说明和C函数，将应填入(n)处的字句写在对应栏内。
【说明】
已知某二叉树的非叶子结点都有两个孩子结点，现将该二叉树存储在结构数组Ht中。结点结构及数组Ht的定义如下：
define MAXLEAFNUM 30
struct node{
char ch; /*当前结点表示的字符，对于非叶子结点，此域不用*/
char *pstr; /*当前结点的编码指针，非叶子结点不用*/
int parent; /*当前结点的父结点，为0时表示无父结点*/
int lchild,rchild;
/*当前结点的左、右孩子结点，为0时表示无对应的孩子结点*/
};
struct node Ht[2*MAXLEAFNUM]; /*数组元素Ht[0]不用*/
该二叉树的n个叶子结点存储在下标为1～n的Ht数组元素中。例如，某二叉树如果其存储结构如下图所示，其中，与叶子结点a对应的数组元素下标为1，a的父结点存储在Ht[5]，表示为Ht[1].parent=5。Ht[7].parent=0表示7号结点是树根，Ht[7].child=3、Ht[7].rchild=6分别表示7号结点的左孩子是3号结点、右孩子是6号结点。
如果用0或1分别标识二叉树的左分支和右分支(如上图所示)，从根结点开始到叶子结点为止，按所经过分支的次序将相应标识依次排列，可得到一个0、1序列，称之为对应叶子结点的编码。例如，上图中a，b，c，d的编码分别是100，101，0，11。
函数LeafCode(Ht[],n)的功能是：求解存储在Ht中的二叉树中所有叶子结点(n个)的编码，叶子结点存储在Ht[1]～Ht[n]中，求出的编码存储区由对应的数组元素pstr域指示。
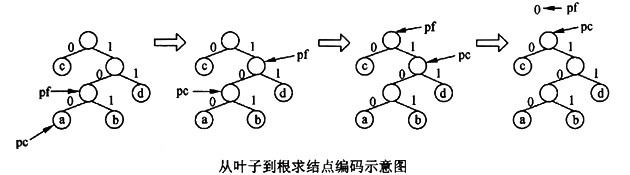
函数LeafCode从叶子到根逆向求叶子结点的编码。例如，对上图中叶子结点a求编码的过程如下图所示。
typedef enum Status {ERROR,OK} Status;
【C函数】
Status LeafCode(struct node Ht[], int n)
{
int pc, pf; /*pc用于指出树中的结点，pf则指出pc所对应结点的父结点*/
int i,start;
char tstr[31] = {'\0'}; /*临时存储给定叶子结点的编码，从高下标开始存入*/
for(i = 1;(1); i++){ /*对所有叶子结点求编码，i表示叶结点在HT数组中的下标*/
start = 29;
pc = i; pf = Ht[i].parent;
while (pf !=(2)) { /*没有到达树根时，继续求编码*/
if ((3).lchild == pc ) /*pc所表示的结点是其父结点的左孩子*/
tstr[--start] = '0';
else
tstr[--start] = '1';
pc =(4); pf = Ht[pf].parent; /*pc和pf分别向根方向回退一层*/
}/* end of while */
Ht[i].pstr = (char *) malloc(31-start);
if (!Ht[i].pstr) return ERROR;
strcpy(Ht[i].pstr,(5));
}/* end of for */
return OK;
}/* and of LeafCode */
相关考题：
阅读以下说明和C语言函数，将应填入(n)处的字句写在答题纸的对应栏内。【说明】一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左子树分支向下查找，直到某个结点不存在左子树时为止，该结点即为此二叉树的“最左下”结点。例如，下图所示的以 A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：typedef stmct BSTNode{int data；struct BSTNode*lch,*rch；//结点的左、右子树指针}*BSTree；函数BSTree Find Del(BSTree root)的功能是：若root指向一棵二叉树的根结点，则找出该结点的右子树上的“最左下”结点*p，并从树于删除以*p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。【函数】BSTrce Find_Del(BSTreeroot){ BSTreep,pre；if ( !root ) return NULL； /*root指向的二叉树为空树*/(1)； /*令p指向根结点的右子树*/if ( !p ) return NULL；(2)； /*设置pre的初值*/while(p-＞lch){ /*查找“最左下”结点*/pre=p；p=(3)；}if ((4)==root) /*root的右子树根为“最左下”结点*/pre-＞rch=NULL；else(5)=NULL； /*删除以“最左下”结点为根的子树*/reurn p；}
阅读以下说明和C语言函数，将应填入(n)处的语句写在对应栏内。【说明】下面的程序构造一棵以二叉链表为存储结构的二叉树。【函数】BitTree *createbt(BitTree *bt){BitTree *q;struct node *s[30];int j,i;char x;printf("i,x=");scant("%d,%c",i,x);while(i!=0 x!='$'){q=(BitTree *}malloc(sizeof(BitTree));//生成一个结点(1);q-＞lchild=NULL;q-＞rchild=NULL;(2) ;if ((3)){j=i/2; // j为i的双亲结点if(i%2==0)(4); //i为j的左孩子else(5); //i为j的右孩子}printf("i,x=");scanf("%d,%c",i,x);}return s[i];}
阅读下列函数说明和C函数，将应填入(n)处的字句写对应栏内。[说明]二叉树的二叉链表存储结构描述如下：typedef struct BiTNode{ datatype data;struct BiTNode *lchild, * rchild; /*左右孩子指针*/}BiTNode,* BiTree;对二叉树进行层次遍历时，可设置一个队列结构，遍历从二叉树的根结点开始，首先将根结点指针入队列，然后从队首取出一个元素，执行下面两个操作：(1) 访问该元素所指结点；(2) 若该元素所指结点的左、右孩子结点非空，则将该元素所指结点的左孩子指针和右孩子指针顺序入队。此过程不断进行，当队列为空时，二叉树的层次遍历结束。下面的函数实现了这一遍历算法，其中Visit(datatype a)函数实现了对结点数据域的访问，数组queue[MAXNODE]用以实现队列的功能，变量front和rear分别表示当前队首元素和队尾元素在数组中的位置。[函数]void LevelOrder(BiTree bt) /*层次遍历二叉树bt*/{ BiTree Queue[MAXNODE];int front,rear;if(bt= =NULL)return;front=-1;rear=0;queue[rear]=(1);while(front (2) ){(3);Visit(queue[front]-＞data); /*访问队首结点的数据域*/if(queue[front]—＞lchild!：NULL){ rear++;queue[rear]=(4);}if(queue[front]-＞rchild! =NULL){ rear++;queue[rear]=(5);}}}
阅读下列函数说明和C函数，将应填入(n)处的字句写在对应栏内。[说明]二叉树的二叉链表存储结构描述如下：lypedef struct BiTNode{ datatype data;street BiTNode *lchiht, *rchild; /*左右孩子指针*/ } BiTNode, *BiTree;下列函数基于上述存储结构，实现了二叉树的几项基本操作：(1) BiTree Creale(elemtype x, BiTree lbt, BiTree rbt)：建立并返回生成一棵以x为根结点的数据域值，以lbt和rbt为左右子树的二叉树；(2) BiTree InsertL(BiTree bt, elemtype x, BiTree parent)：在二叉树bt中结点parent的左子树插入结点数据元素x；(3) BiTree DeleteL(BiTree bt, BiTree parent)：在二叉树bt中删除结点parent的左子树，删除成功时返回根结点指针，否则返回空指针；(4) frceAll(BiTree p)：释放二叉树全体结点空间。[函数]BiTree Create(elemtype x, BiTree lbt, BiTree rbt) { BiTree p;if ((p = (BiTNode *)malloc(sizeof(BiTNode)))= =NULL) return NULL;p-＞data=x;p-＞lchild=lbt;p-＞rchild=rbt;(1);}BiTree InsertL(BiTree bt, elemtype x,BiTree parent){ BiTree p;if (parent= =NULL) return NULL;if ((p=(BiTNode *)malloc(sizeof(BiTNode)))= =NULL) return NULL;p-＞data=x;p-＞lchild= (2);p-＞rchild= (2);if(parent-＞lchild= =NULL) (3);else{p-＞lchild=(4);parent-＞lchild=p;}return bt;}BiTree DeleteL(BiTree bt, BiTree parent){ BiTree p;if (parent= =NULL||parent-＞lchild= =NULL) return NULL;p= parent-＞lchild;parent-＞lchild=NULL;freeAll((5));return bt;
阅读以下预备知识、函数说明和C代码，将应填入(n)处的字句写在对应栏内。[预备知识]①对给定的字符集合及相应的权值，采用哈夫曼算法构造最优二叉树，并用结构数组存储最优二叉树。例如，给定字符集合{a，b，c，d}及其权值2、7、4、5，可构造如图3所示的最优二叉树和相应的结构数组Ht(数组元素Ht[0]不用)(见表5)。结构数组HT的类型定义如下：define MAXLEAFNUM 20struct node {char ch; / * 当前结点表示的字符，对于非叶子结点，此域不用*/int weight; / * 当前结点的权值*/int parent; / * 当前结点的父结点的下标，为0时表示无父结点*/int Ichild, rchild/ *当前结点的左、右孩子结点的下标，为0时表示无对应的孩子结点* /} Ht[2 * MAXLEAFNUM];②用'0'或'1'标识最优二叉树中分支的规则是：从一个结点进入其左(右)孩子结点，就用'0'('1')标识该分支(示例如图3所示)。③若用上述规则标识最优二叉树的每条分支后，从根结点开始到叶子结点为止，按经过分支的次序，将相应标识依次排列，可得到由'0'、'1'组成的一个序列，称此序列为该叶子结点的前缀编码。如图3所示的叶子结点a、b、c、d的前缀编码分别是110、0、111、10。【函数5.1说明】函数void LeafCode (int root, int n)的功能是：采用非递归方法，遍历最优二叉树的全部叶子结点，为所有的叶子结点构造前缀编码。其中形参root为最优二叉树的根结点下标；形参 n为叶子结点个数。在构造过程中，将Ht[p]. weight域用作被遍历结点的遍历状态标志。【函数5.1】char * * Hc;void LeafCode (int root, int n){/*为最优二叉树中的n个叶子结点构造前缀编码，root是树的根结点下标* /int i,p = root,cdlen =0;char code[20];Hc=(char* * )malloc(.(n +]) *sizeof(char* )); /* 申请字符指针数组* /for(i=1;i＜ =p;++i)Ht[ i]. weight =0;/* 遍历最优二叉树时用作被遍历结点的状态标志*/while(p) {/*以非递归方法遍历最优二叉树，求树中每个叶子结点的编码*/if(Ht[p], weight ==0) { /*向左*/Ht[ p]. weight =1if (Ht[p],lchild !=0) { p=Ht[P].lchild; code[cdlen++] ='0';]else if (Ht[p]. rchild ==0) {/* 若是叶子结点，则保存其前缀编码*/Hc[p] = ( char * ) malloc( (cdlen + 1 ) * sizeof (char) );(1); strcpy(He[ p] ,code);}}else if (Ht[ pi, weight == 1) { /*向右*/Ht[p]. weight =2;if(Ht[p].rchild !=0) {p=Ht[p].rchild; code[cdlen++] ='1';}}else{/* Ht[p]. weight ==2,回退*/Ht[p]. weight =0;p=(2);(3); /*退回父结点*/}}/* while结束* /}【函数5.2说明】函数void Decode(char*buff, int root)的功能是：将前缀编码序列翻译成叶子结点的字符序列并输出。其中形参root为最优二叉树的根结点下标；形参buff指向前缀编码序列。【函数5.2】void Decode( char * buff, int root)Iint pre =root,p;while ( * buff! = '\0') {p = root;while (p!=0){/*存在下标为p的结点*/pre=p;if((4))p=Ht[p].lchild; /*进入左子树*/else p = Ht[p]. rchild; / *进入右子树*./buff ++; / * 指向前缀编码序列的下一个字符* /}(5);printf("%c", Ht [ pre]. ch);}}
阅读以下说明、C函数和问题，将解答填入答题纸的对应栏内。【说明】二叉查找树又称为二叉排序树，它或者是一棵空树，或者是具有如下性质的二叉树：●若它的左子树非空，则其左子树上所有结点的键值均小于根结点的键值;●若它的右子树非空，则其右子树上所有结点的键值均大于根结点的键值;●左、右子树本身就是二叉查找树。设二叉查找树采用二叉链表存储结构，链表结点类型定义如下：typedefstructBiTnode{intkey_value;/*结点的键值，为非负整数*/structBiTnode*left,*right;/*结点的左、右子树指针*/}*BSTree;函数find_key(root,key)的功能是用递归方式在给定的二叉查找树(root指向根结点)中查找键值为key的结点并返回结点的指针;若找不到，则返回空指针。【函数】BSTreefind_key(BSTreeroot,intkey){if((1))returnNULL;elseif(key==root-key_value)return(2);elseif(keykey_value)return(3);elsereturn(4);}【问题1】请将函数find_key中应填入(1)~(4)处的字句写在答题纸的对应栏内。【问题2】若某二叉查找树中有n个结点，则查找一个给定关键字时，需要比较的结点个数取决于(5).
阅读以下说明和C语言函数，将应填入(n)处的字句写在对应栏内。【说明】下面的程序构造一棵以二叉链表为存储结构的二叉树算法。【函数】BTCHINALR *createbt ( BTCHINALR *bt ){BTCHINALR *q;struct node1 *s [30];int j,i;char x;printf ( "i,x =" ); scanf ( "%d,%c",i,x );while (i!=0 x!='$'){ q = ( BTCHINALR* malloc ( sizeof ( BTCHINALR )); //生成一个结点(1);q-＞1child = NULL;q-＞rchild = NULL;(2);if((3);){j=i/2 //j为i的双亲结点if(i%2==0(4) //i为j的左孩子else(5) //i为j的右孩子}printf ( "i,x =" ); scanf ( "%d,%c",i,x ); }return s[1]}
●试题五阅读以下预备知识、函数说明和C代码，将应填入(n)处的字句写在答题纸的对应栏内。【预备知识】①对给定的字符集合及相应的权值，采用哈夫曼算法构造最优二叉树，并用结构数组存储最优二叉树。例如，给定字符集合{a，b，c，d}及其权值2、7、4、5，可构造如图3所示的最优二叉树和相应的结构数组Ht(数组元素Ht［0］不用)(见表5)。图3最优二叉树表5 结构数组Ht结构数组Ht的类型定义如下：define MAXLEAFNUM 20struct node{char ch;/*当前结点表示的字符，对于非叶子结点，此域不用*/int weight;/*当前结点的权值*/int parent;/*当前结点的父结点的下标，为0时表示无父结点*/int lchild,rchild;/*当前结点的左、右孩子结点的下标，为0时表示无对应的孩子结点*/}Ht［2*MAXLEAFNUM］;②用′0′或′1′标识最优二叉树中分支的规则是：从一个结点进入其左(右)孩子结点，就用′0′(′1′)标识该分支(示例如图3所示)。③若用上述规则标识最优二叉树的每条分支后，从根结点开始到叶子结点为止，按经过分支的次序，将相应标识依次排列，可得到由′0′、′1′组成的一个序列，称此序列为该叶子结点的前缀编码。例如图3所示的叶子结点a、b、c、d的前缀编码分别是110、0、111、10。【函数5．1说明】函数void LeafCode(int root,int n)的功能是：采用非递归方法，遍历最优二叉树的全部叶子结点，为所有的叶子结点构造前缀编码。其中形参root为最优二叉树的根结点下标；形参n为叶子结点个数。在构造过程中 ，将Ht［p］．weight域用作被遍历结点的遍历状态标志。【函数5．1】char**Hc；void LeafCode(int root,int n){/*为最优二叉树中的n个叶子结点构造前缀编码，root是树的根结点下标*/int i,p=root,cdlen=0;char code［20］;Hc=(char**)malloc((n+1)*sizeof(char*));/*申请字符指针数组*/for(i=1;i＜=p;++i)Ht［i］．weight=0;/*遍历最优二叉树时用作被遍历结点的状态标志*/while(p){/*以非递归方法遍历最优二叉树，求树中每个叶子结点的编码*/if(Ht［p］．weight==0){/*向左*/Ht［p］．weight=1;if (Ht［p］．lchild !=0) { p=Ht［p］．lchild; code［cdlen++］=′0′;}else if (Ht［p］．rchild==0) {/*若是叶子结 点，则保存其前缀编码*/Hc［p］=(char*)malloc((cdlen+1)*sizeof(char));(1) ;strcpy(He［p］，code);}}else if (Ht［p］．weight==1){/*向右*/Ht［p］．weight=2;if(Ht［p］．rchild !=0){p=Ht［p］．rchild;code［cdlen++］=′1′;}}else{/*Ht［p］．weight==2,回退*/Ht［p］．weight=0;p= (2) ; (3) ;/*退回父结点*/}}/*while结束*/}【函数5．2说明】函数void Decode(char*buff,int root)的功能是：将前缀编码序列翻译成叶子结点的字符序列并输出。其中形参root为最优二叉树的根结点下标;形参buff指向前缀编码序列。【函数5．2】void Decode(char*buff,int root){ int pre=root,p;while(*buff!=′＼0′){p=root;while(p!=0){/*存在下标为p的结点*/pre=p;if( (4) )p=Ht［p］．lchild;/*进入左子树*/else p=Ht［p］．rchild;/*进入右子树*/buff++;/*指向前缀编码序列的下一个字符*/｝(5) ;printf(″%c″,Ht［pre］．ch);}}
试题三（共 15 分）阅读以下说明和 C 程序，将应填入 （n） 处的字句写在答题纸的对应栏内。