考虑完全竞争市场里的某厂商,其短期生产函数为其中L是可变生产要素,K是固定生产要素,令L的价格为PL>O。 (1)结合图形和公式,说明生产的三个阶段划分的标准。 (2)若PL—PK,则最优要素组合应该在第几阶段进行?其具体位置如何选择?
考虑完全竞争市场里的某厂商,其短期生产函数为
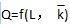
其中L是可变生产要素,K是固定生产要素,令L的价格为PL>O。 (1)结合图形和公式,说明生产的三个阶段划分的标准。 (2)若PL—PK,则最优要素组合应该在第几阶段进行?其具体位置如何选择?
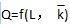
其中L是可变生产要素,K是固定生产要素,令L的价格为PL>O。 (1)结合图形和公式,说明生产的三个阶段划分的标准。 (2)若PL—PK,则最优要素组合应该在第几阶段进行?其具体位置如何选择?
参考解析
解析:(1)短期生产的三个阶段是在假定生产技术水平和其他要素投入量不变,只有劳动投入可变的条件下,以劳动投入多少来划分的生产不同阶段。具体而言,短期生产的三个阶段是根据总产量曲线、平均产量曲线和边际产量曲线之间的关系来划分的。如图1-1所示:第1阶段,平均产量递增阶段,即劳动平均产量始终是上升的,且达到最大值。这一阶段是从原点到APL、MPL两曲线的交点,即劳动投入量由0到L3的区间。第Ⅱ阶段,平均产量的递减阶段,但边际产量仍然大于0,所以总产量仍然是递增的,直到总产量达到最高点。这一阶段是从APL、MPL两曲线的交点到MPL曲线与横轴的交点,即劳动投入量由L3到L4的区间。第Ⅲ阶段,边际产量为负,总产量也是递减的,这一阶段是MPL曲线和横轴的交点以后的阶段,即劳动投入量L4以后的区间。
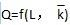
图1-1 -种可变生产要素的生产函数的产量曲线 (2)首先,厂商肯定不会在第Ⅲ阶段进行生产,因为这个阶段的边际产量为负值,生产不会带来任何的好处。其次,厂商也不会在第1阶段进行生产,因为平均产量在增加,投人的这种生产要素还没有发挥最大的作用,继续扩大可变投入的使用量从而使产量扩大是有利可图的。因此厂商通常会在第Ⅱ阶段进行生产,虽然平均产量和边际产量都下降,但是总产量还在不断增加,收入也增加,只是增加的速度逐渐减慢,直到停止增加时为止。短期中,资本不可变,劳动可变,应调整劳动数量以实现利润最大化,即应满足
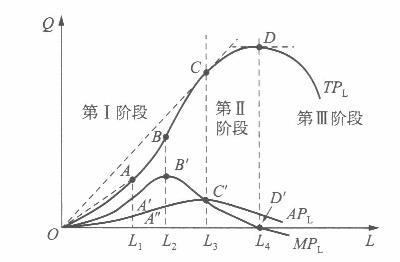
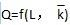
图1-1 -种可变生产要素的生产函数的产量曲线 (2)首先,厂商肯定不会在第Ⅲ阶段进行生产,因为这个阶段的边际产量为负值,生产不会带来任何的好处。其次,厂商也不会在第1阶段进行生产,因为平均产量在增加,投人的这种生产要素还没有发挥最大的作用,继续扩大可变投入的使用量从而使产量扩大是有利可图的。因此厂商通常会在第Ⅱ阶段进行生产,虽然平均产量和边际产量都下降,但是总产量还在不断增加,收入也增加,只是增加的速度逐渐减慢,直到停止增加时为止。短期中,资本不可变,劳动可变,应调整劳动数量以实现利润最大化,即应满足

相关考题:
计算题:已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求: 计算题:已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场上价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数
已知某个完全竞争行业中的单个厂商的短期成本函数是STC=0.1Q3—2Q2+15Q+10。求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
在完全竞争市场下,某厂商的需求函数和供给函数分别为:Q=5 000-200P 和Q=4 000+300P。以下说法正确的是( )。A.该厂商的市场均衡价格为P=4B.该厂商的市场均衡产量为Q=4 600C.该厂商的市场均衡产量为Q=4 500D.该厂商的市场均衡价格为P=2
假定某完全竞争行业有100个相同的厂商,单个厂商的短期总成本函数为.STC=Q2+6Q +20。 (l)求市场的短期供给函数。 (2)假定市场的需求函数为Qd=420 - 30P,求该市场的短期均衡价格和均衡产量。 (3)假定政府对每一单位商品征收1.6元的销售税,那么,该市场的短期均衡价格和均衡产量是多少?消费者和厂商各自负担多少税收?
已知某完全竞争行业中的单个厂商的短期成本函数为STC =0.1Q3- 2Q2+150 +10 . (1)求当市场上产品的价格为P=55时,厂商的短期均衡产量和利润。 (2)当市场价格下降为多少时,厂商必须停产? (3)求厂商的短期供给函数。
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时候企业个数
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。
完全竞争行中某厂商的成本函数为TC=Q3-6Q2+30Q+40试求: (1)假设产品价格为66元,利润最大化时的产量及利润总额。 (2)竞争市场供求发生变化,由此决定的新价格为30元,在新价格下,厂商是否会发生亏损?如果会,最小的亏损额为多少? (3)该厂商在什么情况下会停止生产? (4)厂商的短期供给函数。
完全竞争市场中某厂商的短期成本函数为 ,若产品售价为82,请 计算: (1)利润最大化时的产量和利润。 (2)若市场条件发生变化,均衡价格下降到19,此时厂商是否会亏损?若亏损,其最小亏损额是多少? (3)在上述问题(2)中,厂商是否会停产,为什么?
假设某完全竞争行业有500个相同的厂商,每个厂商的短期成本函数为:STC=O. 5Q2+Q+10。 (1)求完全竞争市场的短期供给函数。 (2)假设市场需求函数为QD=4 000-400P,求市场的均衡价格和产量。 (3)假定对每一件产品征收0.9元的税,新的市场均衡价格和产量又为多少?厂商和消费者的税收负担各为多少?
完全竞争市场上,厂商生产要素为x1,x2,面对的是竞争性要素需求市场,两种要素的价格都为2,每个企业的固定成本为64。单个厂商的生产函数为消费者对该产品的需求函数为Q=280-5p,其中p为产品的市场价格 长期均衡时的单个企业产量和价格
问答题计算题: 已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3-2Q2+15Q+10。试求: (1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润; (2)当市场上价格下降为多少时,厂商必须停产; (3)厂商的短期供给函数
问答题已知完全竞争市场的需求函数为D=6300-400P,短期市场供给函数为SS=3000+150P,单个企业在LAC曲线最低点的价格为6,产量为50,单个企业的成本规模不变。 求:(1)市场短期均衡价格与均衡产量。 (2)判断该市场是否同时处于长期均衡,求行业内的厂商数量。 (3)如果市场的需求函数变为D′=8000-400P,短期供给函数SS′=4700+150P,求市场短期均衡的价格和产量。 (4)判断该市场是否同时处于长期均衡,并求行业内厂商数量。
问答题已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q3—2Q2+15Q+10。试求:(1)当市场上产品的价格为P=55时,厂商的短期均衡产量和利润;(2)当市场价格下降为多少时,厂商必须停产;(3)厂商的短期供给函数。
问答题已知某完全竞争行业中的单个厂商的短期成本函数为:STC=0.1Q3-2Q2+15Q+10(1)当市场上产品价格为 55时厂商的短期均衡产量和利润;(2)当市场价格下降为多少时厂商必须停产?(3)求厂商的短期供给函数。