已知消费者的效用函数为U=αlnx1+x2,请写出在P1=2,p2 =4,y=10,a=1/3时p2变化对于x1(p,y)的替代效应和收入效应。其中p1、p2分别代表两种物品x1、x2的价格,y代表消费者的收入水平。如果p2从4上升为p'2 =5,P1保持不变,那么为了使该消费者效用水平(用U表示)保持不变,应该如何对该消费者进行补偿?
已知消费者的效用函数为U=αlnx1+x2,请写出在P1=2,p2 =4,y=10,a=1/3时p2变化对于x1(p,y)的替代效应和收入效应。其中p1、p2分别代表两种物品x1、x2的价格,y代表消费者的收入水平。如果p2从4上升为p'2 =5,P1保持不变,那么为了使该消费者效用水平(用U表示)保持不变,应该如何对该消费者进行补偿?
参考解析
解析:根据拟线性效用函数性质求解。消费者的效用最大化问题为:
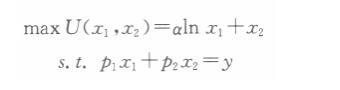
求解可得:

设商品x2的价格变化量为
△p2,即p'2=p2 +△p2,则此时

从而替代效应=总效应=

收入效应为0。 若p'2=5,则替代效应为1/6(2)由(1)可得马歇尔需求函数为:
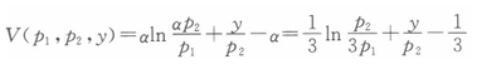
支出函数为:

为使效用

保持不变,则消费者补偿为:

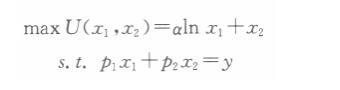
求解可得:

设商品x2的价格变化量为
△p2,即p'2=p2 +△p2,则此时

从而替代效应=总效应=

收入效应为0。 若p'2=5,则替代效应为1/6(2)由(1)可得马歇尔需求函数为:
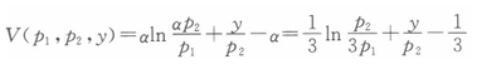
支出函数为:

为使效用

保持不变,则消费者补偿为:

相关考题:
已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2=30元,该消费者的效用函数为U=3X1X22,该消费者每年购买这两种商品的数量各应是多少?每年从中获得总效用是多少?
有以下程序: float f1(float n) { return n*n; } float f2(float n) { return 2*n; } main() {float(*p1)(float),(*p2)(float),(*t)(float),y1,y2; p1:f1; p2=f2; y1=p2(p1(2.0)); t=p1; p1=p2; p2=t; y2=p2(p1(2.0)); printf("%3.0f,%3.0f\n",y1,y2); } 程序运行后的输出结果是 ______。A.8, 16B.8, 8C.16, 16D.4, 8
分析下面的程序 main() { int*p1,*p2,*p; int x=4,y=6; p1=x;p2=y; if(x<y) {p=p1;p1=p2;p2=p; } printf("%d,%d,",*p1,*p2); printf("%d,%d\n",x,y); } 程序的输出结果为_______。A.6,4,4,6B.4,6,6,4C.4,6,4,6D.6,4,6,4
有以下程序 float fl(float n) { return n*n; } float f2(float n) { return 2*n;} main() {float(*p1)(float),(*p2)(float),(*t)(float),y1,Y2; p1=f1; p2=f2; y1=p2(p1(2.O)); t=p1; p1=p2; p2=t; y2=p2(pl(2.0)); printf("%3.0f,%3,Of\n",y1,y2); } 程序运行后的输出结果是A.8,16B.8,8C.16,16D.4,8
消费者显示了对于商品1和商品2的如下需求: 价格为(p1,p2)=(2,4)时,需求为(q1,q2)-(1,2);价格为(p1,p2)=(6,3)时,需求为(q1,q2)一(2,1)。该消费者的选择是与其效用最大化目标一致的。
在一个人(既是消费者又是生产者)的经济e={X,y,ω}中,商品1和商品2在消费和生产中分别满足下面的条件:X一{z∈R2 ▏x1≥2,x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0)。效用函数为U(x1,x2)-(x1-2)x2,初始资源禀赋为ω=(4,0)。 对于价格p=(p1,p2)∈R2++,写出生产者问题并求解最大化利润下的y1和y2。
在一个人(既是消费者又是生产者)的经济e={X,y,ω}中,商品1和商品2在消费和生产中分别满足下面的条件:X一{z∈R2 ▏x1≥2,x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0)。效用函数为U(x1,x2)-(x1-2)x2,初始资源禀赋为ω=(4,0)。假设财富满足ω≥2P1, 对于P=(p1,p2)∈R2++写出消费者问题并求解对x1和x2的需求量。
己知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P1=20元和P2= 30元,该消费者的效用函数为该消费者每年购买这两种商品的数量应各是多少每年从中获得的总效用是多少?
在一个人(既是消费者又是生产者)的经济e={X,y,ω}中,商品1和商品2在消费和生产中分别满足下面的条件:X一{z∈R2 ▏x1≥2,x2≥0}Y={y∈R2▏y2≤2(-y1)2,y1≤0)。效用函数为U(x1,x2)-(x1-2)x2,初始资源禀赋为ω=(4,0)。现在假设财富取决于初始禀赋和利润,请推导出商品1的市场均衡条件。假如此时p1=1,p2为多少?
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 如果第一种商品价格由1提高为2,其他因素不变,则价格上升对第一种商品的消费量影响的总效应有多少?按照Slutsky分解原理,收入效应和替代效应分别是多少?
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 计算第一种商品价格从1变化为2,要保持原有效应不变的收入补偿数额。
已知某消费者的效用函数为U=X1X2,两商品的价格分别为P1=4、P2=2,消费者的收入是M=80.现在假定商品1的价格下降为P1=2.求: (1)由商品1的价格P1下降导致的总效应,使得该消费者对商品1的购买量发生多少变化? (2)由商品1的价格P1下降导致的替代效应,使得该消费者对商品1的购买量发生多少变化? (3)由商品1的价格P1下降导致的收入效应,使得该消费者对商品1的购买量发生多少变化?
某消费者的效用函数为u(x1.x2)一√五云,商品x1和x2的价格为P1和P2,收入为ya (1)假设商品x1和x2的价格为P1=l和P2=2,该消费者收入为y=100。求该消费者对两种商 品的需求量。 (2)若商品x1价格升至2,即此时P1=P2 =2,该消费者收入不变。求此价格变化对商品Xl产生的替代效应和收入效应。
某消费者的效用函数为U=(x1,x2)=x11/3x2/3,x1和x2分别为两种商品的消费量,消费者收入为100,两种商品现在价格分别为P1=1,P2=2,求: 消费者最优消费的xi和xo量。
假设消费者用既定的收入w购买两种商品,P1和P2分别为两种商品的既定价格,以Q1和Q2分别表示两种商品的数量,则P1Q1+P2Q2=w;MU1和MU2分别表示两种商品的边际效用,λ表示每一元货币带来的边际效用,则消费者效用最大化的均衡条件为( )。A.MU1/P2=MU2/P1=λB.MU1/P1=MU2/P2=λC.P1/MU1=P2/MU2=λD.P2/MU1=P1/MU2=λ
设X~N(μ,42),Y~N(μ,52),p1=P{X≤μ-4},p2=P{Y≥μ+5},则()A、对任意实数,都有p1=p2B、对任意实数,都有p12C、对任意实数,都有p1p2D、对任意实数,都有p1≠p2
两电阻串联,已知R1/R2=1/2,则电阻上的电压之比U1/U2.功率之比P1/P2分别是()。A、U1/U2=1/2,P1/P2=2B、U1/U2=2,P1/P2=4C、U1/U2=1/2,P1/P2=1/2D、U1/U2=1/2,P1/P2=1/4
已知消费者的收入为I,全部用来购买X1,X2,且MU1/P1>MU2/P2,若要达到消费者均衡,需要()A、增加的X1购买,减少X2的购买B、增加X2的购买,减少X1的购买C、X1,X2都增加D、X1,X2都减少。
问答题根据序数效用论的消费者均衡条件,在MRS12>P1/P2或MRS12<P1/P2时,消费者应如何调整两商品的购买量?为什么?