相关系数r与回归系数b的关系为()。
相关系数r与回归系数b的关系为()。


参考解析
解析: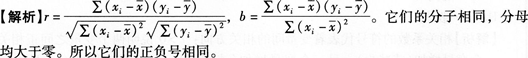
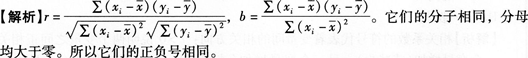
相关考题:
从样本得到变量X与Y的相关系数r=0.92,则 A、X与Y之间一定存在因果关系B、若对此份资料作回归分析,其回归系数是正值C、若对此份资料作回归分析,其回归系数是负值D、表明总体相关系数 p≠0E、表明总体相关系数 p=0
由n个数组(xi,yi。)计算得 Lxx=330,Lxy=-l68,Lyy=9.4 由此可以看出( )。A.x与y,的相关系数r0B.x与Y的相关系r0C.Y对x的回归系数b0D.y对x的回归系数b0E.相关系数r与回归系数异号
由n个数组(xi,yi)计算得Lxx= 330,_Lxy=﹣168,Lyy= 9.4由此可以看出( )。A. x与y的相关系数r>0B.工与y的相关系数rC. y对x的回归系数b>0 D. y对x的冋归系数bE.相关系数r与回归系数b异号
由n个数组(xi,yi)计算得Lxx= 330, Lxy =-168,Lxy=9.4由此可以看出()。 A. X与y,的相关系数r>0B. X与y的相关系数rC. y与x对r的回归系数b>0D. y对x的回归系数bE.相关系数r与回归系数异号
相关系数与回归系数()A、回归系数大于零则相关系数大于零B、回归系数小于零则相关系数小于零C、回归系数大于零则相关系数小于零D、回归系数小于零则相关系数大于零E、回归系数等于零则相关系数等于零
多选题相关系数与回归系数( )。A回归系数大于零则相关系数大于零B回归系数小于零则相关系数小于零C回归系数大于零则相关系数小于零D回归系数小于零则相关系数大于零E回归系数等于零则相关系数等于零
单选题从样本得到变量X与Y的相关系数r=0.92,则()。AX与Y之间一定存在因果关系B若对此份资料作回归分析,其回归系数是正值C若对此份资料作回归分析,其回归系数是负值D表明总体相关系数p≠0E表明总体相关系数p=0
判断题回归系数b的符号与相关系数r的符号,可以相同也可以不相同。A对B错