某企业生产的某种产品在市场上供不应求,因此该企业决定投资扩建新厂。据研究分析,该产品10年后将升级换代,目前的主要竞争对手也可能扩大生产规模,故提出以下三个扩建方案:1.大规模扩建新厂,需投资3亿元。据估计,该产品销路好时,每年的净现金流量为9000万元;销路差时,每年的净现金流量为3000万元。2.小规模扩建新厂,需投资1.4亿元。据估计,该产品销路好时,每年的净现金流量为4000万元;销路差时,每年的净现金流量为3000万元。3.先小规模扩建新厂,3年后,若该产品销路好再决定是否再次扩建。若再次扩建,需投资2亿元,其生产能力与方案1相同。据预测,在今后10年内,该产品销路好的概率为0.7,销路差的概率为0.3。基准折现率 ic=10%,不考虑建设期所持续的时间。【问题】1.画出决策树。2.试决定采用哪个方案扩建。
某企业生产的某种产品在市场上供不应求,因此该企业决定投资扩建新厂。据研究分析,该产品10年后将升级换代,目前的主要竞争对手也可能扩大生产规模,故提出以下三个扩建方案:
1.大规模扩建新厂,需投资3亿元。据估计,该产品销路好时,每年的净现金流量为9000万元;销路差时,每年的净现金流量为3000万元。
2.小规模扩建新厂,需投资1.4亿元。据估计,该产品销路好时,每年的净现金流量为4000万元;销路差时,每年的净现金流量为3000万元。
3.先小规模扩建新厂,3年后,若该产品销路好再决定是否再次扩建。若再次扩建,需投资2亿元,其生产能力与方案1相同。据预测,在今后10年内,该产品销路好的概率为0.7,销路差的概率为0.3。基准折现率 ic=10%,不考虑建设期所持续的时间。

【问题】
1.画出决策树。
2.试决定采用哪个方案扩建。
参考解析
l.根据背景资料所给出的条件画出决策树,标明各方案的概率和净现金流量,如下图所示。
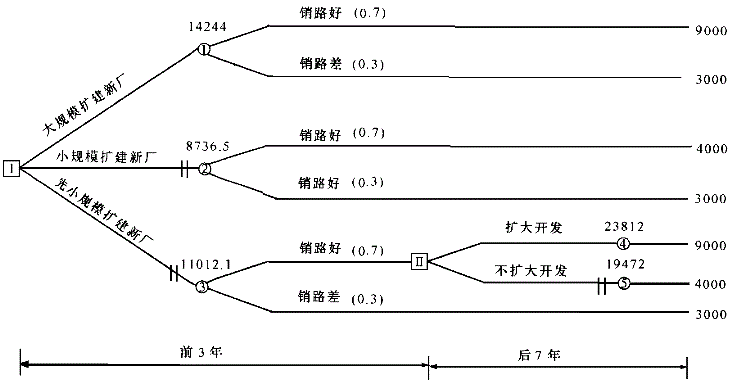
决策树
2.计算上图中各机会点的期望值(将计算结果标在各机会点上方)
点①:[(9000×0.7+3000×0.3)×(P/A,10%,10)-30000]万元=(7200×6.145-30000)万元=14244万元
点②:[(4000×0.7+3000×0.3)×(P/A,10%,10)-14000]万元=(3700×6.145-14000)万元=8736.5万元
点④:[9000×(P/A,10%,7)-20000]万元=(9000×4.868-20000)万元=23812万元
点⑤:4000×(P/A,10%,7)万元=(4000×4.868)万元=19472万元
对于决策点II,机会点④的期望值大于机会点⑤的期望值,因此应采用3年后销路好时再次扩建的方案。机会点③期望值的计算比较复杂,包括以下两种状态下的两个方案:
(1)销路好状态下的前3年小规模扩建,后7年再次扩建。
(2)销路差状态下小规模扩建持续10年。故机会点③的期望值为:
[4000×0.7×(P/A,10%,3)+23812×0.7×(P/F,10%,3)+3000×0.3×(P/A,10%,10)-14000]万元
=(4000×0.7×2.487+23812×0.7×0.751+3000×0.3×6.145)万元
=11012.1万元
对于决策点I的决策,需比较机会点①、②、③的期望值,由于机会点①的期望值最大,故应采用大规模扩建新厂方案。