图示两端铰支压杆的截面为矩形，当其失稳时：

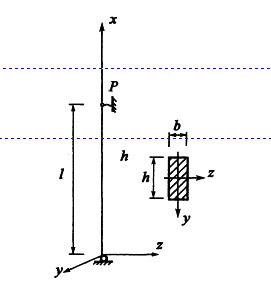
图示两端铰支压杆的截面为矩形，当其失稳时：


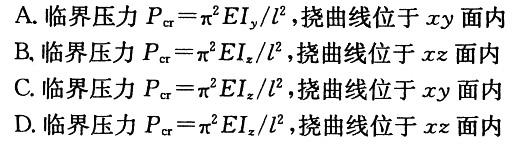
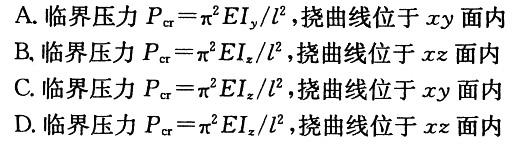
参考解析

解析：解根据临界压力的概念，临界压力是指压杆由稳定开始转化为不稳定的最小轴向压

相关考题：

同一长度的压杆，截面积及材料均相同，仅两端支承条件不同，则（ ）杆的临界力最小。A．两端铰支 B．一端固定，一端自由 C．一端固定，一端铰支 D．两端同定
查看答案
两端铰支的圆截面压杆,长1m,直径50mm。其柔度为() A.60;B. 66.7;C.80;D.50
查看答案
两端铰支理想细长压杆在临界轴力作用下失稳时,其挠曲线为半波正弦曲线。() 此题为判断题(对，错)。
查看答案
图示两端铰支压杆的截面为矩形，当其失稳时：
查看答案
图示矩形截面细长(大柔度)压杆，弹性模量为E。该压杆的临界荷载Fcr为：
查看答案
图示矩形截面细长(大柔度)压杆，弹性模量为E。该压杆的临界载荷Fσ
查看答案
图示两端较支压杆的截面为矩形，当其失稳时：
查看答案
图示两端铰支压杆的截面为矩形，当其失稳时：A.临界压力Pcr=π2EIy/l2，挠曲线位于xy面内B.临界压力Pcr=π2EIz/l2，挠曲线位于xz面内C.临界压力Pcr=π2EIz/l2，挠曲线位于xy面内D.临界压力Pcr=π2EIz/l2，挠曲线位于xz面内
查看答案
图示两端铰支压杆的截面为矩形，当其失稳时： A.临界压力Pcr=π2EI∥ι^2，挠曲线位于xy面内B.临界压力Pcr=π2EI∥ι^2，挠曲线位于xy面内C.临界压力Pcr=π2EI∥ι^2，挠曲线位于xy面内D.临界压力Pcr=π2EI∥ι^2，挠曲线位于xz面内
查看答案
一端固定，一端为球形铰的大柔度压杆，横截面为矩形，则该杆临界力Pcr为：
查看答案
关于压杆稳定的说法，错误的是（ ）。A.材料弹性模量小则更易失稳B.压杆的截面小则更易失稳C.压杆的长度小则更易失稳D.两端铰接杆比两端固定杆更易失稳
查看答案
采用()截面作为压杆的材料，其抗失稳能力差。A.矩形B.方形C.圆形D.圆管形
查看答案
同一长度的压杆，截面积及材料均相同，仅两端支承条件不同，则（ ）杆的临界力最大。 A、两端铰支 B、一端固定，一端自由 C、一端固定，一端铰支 D、两端固定
查看答案
如图5-69所示，两端球铰的正方形截面压杆，当失稳时，截面将绕哪个轴转动为( )。A.绕y轴弯曲 B.绕z1轴弯曲C.绕z轴弯曲 D.可绕过形心C的任何轴弯曲
查看答案
同一长度的压杆，截面积及材料均相同，仅两端支承条件不同：①两端固定；②一端固定，一端铰支；③两端铰支；④一端固定，一端自由；则杆的临界力从大到小排列的是（）。A、①②③④B、④③②①C、①③②④D、④①③②
查看答案
两端固定时的压杆临界力大于两端铰支时的临界力。
查看答案
两端铰支等截面细长压杆的长度因数为（）。A、0.5B、0.7C、1D、2
查看答案
一细长压杆，已知压杆的长度为1m，一端固定，一端铰支，其横截面为圆形，直径为20mm。则该压杆的惯性半径i=（），柔度λ=（）。
查看答案
计算两端铰支细长压杆的临界载荷时，惯性矩应采用横截面的最小惯性矩。
查看答案
两端铰支的圆截面压杆，长1m，直径50mm。其柔度为（）。A、60B、66.7C、80D、50
查看答案
同样面积的杆件截面，做成（）截面比实心圆形的压杆不易失稳。A、矩形B、环形C、方形D、工字形
查看答案
用（）截面作为压杆的材料，其抗失稳能力差。A、矩形B、方形C、圆形D、圆管形
查看答案
同一长度的压杆，截面面积及材质均相同，仅两端支承条件不同，则压杆临界力最小的情况是（）A、两端铰支B、一端固定，一端自由C、两端固定D、一端固定，一端铰支
查看答案
相同材料、长度、截面的压杆在下列支撑条件下临界值最小的是（）。A、两端铰支B、一端固定，一端自由C、两端固定D、一端固定，一端铰支
查看答案
两端铰支压杆失稳时杆的曲线是（）。A、二次曲线B、余弦曲线C、三次曲线D、正弦曲线
查看答案
单选题用（）截面作为压杆的材料，其抗失稳能力差。A矩形B方形C圆形D圆管形
查看答案
单选题两端铰支压杆失稳时杆的曲线是（）。A二次曲线B余弦曲线C三次曲线D正弦曲线
查看答案
单选题同一长度的压杆，截面面积及材质均相同，仅两端支承条件不同，则压杆临界力最小的情况是（）A两端铰支B一端固定，一端自由C两端固定D一端固定，一端铰支
查看答案
热门标签